2. 中国消防救援学院, 北京 102202;
3. 应急管理部国家自然灾害防治研究院, 北京 100085
2. China Fire and Rescue College, Beijing 102202, China;
3. National Institute of Natural Hazards, Ministry of Emergency Management, Beijing 100085, China
超大型城市(城区常住人口1000万以上)是周边城市群发展核心,人口资源高度密集,社会经济高度发达(赵小伟等,2022),这些优势资源在给城市带来各种机遇的同时,也面临诸多挑战(马鸿雁,2021),一旦发生重大地震灾害,极易给国家和人民造成巨大损失,并且超大型城市其地震灾害发生的破坏性及连锁性均远大于非城市地区。地震巨灾发生后,超大型城市的震害情景具有信息不对称性、蔓延性、复杂性、社会性、双重性等特点,给震后的应急响应增添了难度。针对超大型城市地震巨灾,需要采取“底线思维”,最大限度地应对最坏情景的发生,并做好充分的准备,提高超大型城市应对地震巨灾的应对能力。
鉴于无法从真实案例中研究地震巨灾全流程应急响应任务的特殊性,本文将采取情景构建方法,以研究地震灾害应急响应为出发点,明确灾害应急响应建设的主要任务和方向。情景构建方法从多角度、全过程模拟应急管理所面临的场景,从而分解应急需求和任务,这与应急管理四阶段论相契合,可完整展现情景事件的孕育、爆发、演化和恢复各阶段的工作重点,并细化出任务清单,供应急工作人员查漏补缺,完整准确地对应急管理各项工作做出安排,有效提升应急管理效果(盖程程,2020)。刘铁民(2012)首次在国内开展情景构建研究,提出基于“情景-任务-能力”的应急预案编制方法,有效引导和推进了应急工作进程。王慧彦等(2016)基于情景构建的优势,提出了适合我国应急体系的地震巨灾准备规划框架。随后,王慧彦(2017)又提出城市功能系统安全视域下的地震情景研究,提升了地震应急响应与应急防御体系的跨区域联动能力和跨部门协同治理能力。为解决跨区域应急救援问题,王慧彦等(2023)引入了“目标-行动-反馈-调整”的质量管理循环模型,构建了京津冀地区跨区域地震应急协同流程。张文静等(2018)提出重大突发事件情景构建理论,通过假设某地发生重大地震灾害事件,对震害描述、应急响应等任务进行实例分析。虽然情景构建方法能够模拟各种不同的震害情景,但在超大型城市地震巨灾情景中,由于次生衍生灾害的复杂性和多变性,导致应急资源调配、生命线系统抢险等方面的应急响应存在不确定性因素。目前对于震害情景中不确定问题的研究较少,需要对其进行进一步完善。
本文在情景构建的基础上,通过对地震灾害及其发生机理、震害情景的设想(朱伟等,2019),对历史灾害和现代城市基础数据进行聚类、总结,提出了一种模糊推演方法,将不确定的震情信息与模糊规则进行匹配,按照时间序列描述事件发生机理及推演次生衍生灾害,判断情景推演事件发生的可能性及结果的严重性,对事件情景的优先级和重要程度进行排序,进而为决策者提供决策依据。
1 研究思路情景构建主要是对黑天鹅事件(即小概率、高风险事件)进行灾害情景描述,包括诱发因素、破坏情况、波及范围、灾害链及其后果等,并依此明确应急响应的目标及任务(朱伟等,2019)。情景构建可以作为决策者对地震巨灾事件进行应急决策的基础和依据,而情景要素则作为情景构建的前期工作,将错综复杂的事件进行梳理,归纳出情景要素(高山等,2021)。推演震害全过程与各方面的合理假设是情景推演的重要内容,也是地震应急管理研究的必要组成部分。
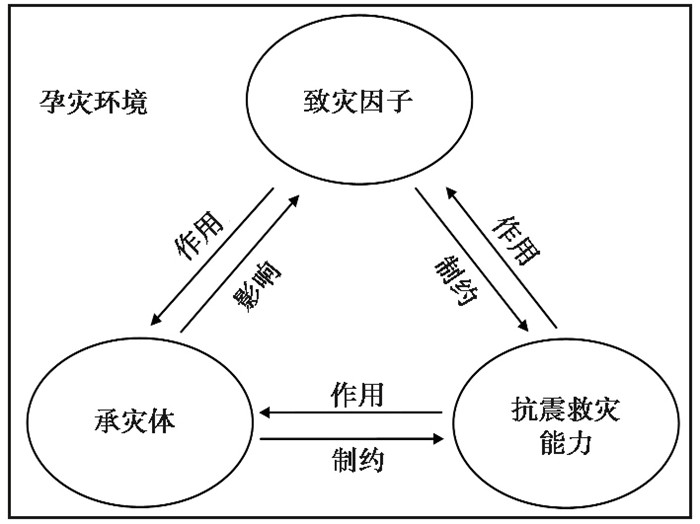
1.1 情景要素情景的主要目的是辅助决策者对突发事件开展快速、高效的决策,情景不止包含自然界中客观存在的因素,还涵盖决策者或受灾群众的一些主观性活动,如对紧急情况的应对能力(周愉峰等,2020)。因此,本文认为地震灾害情景的要素主要由四方面构成,即致灾因子、孕灾环境、承灾体以及抗震救灾能力(刘健等,2016),如图 1所示。其中,致灾因子表示引发地震灾害的致灾因素的集合,如地震加速度等;孕灾环境是指地震灾害后的外部环境因素集合,其中包含地理环境、社会因素及人文影响,如地质构成、经济发展、风俗文化等;承灾体是各种致灾因子作用对象的集合,如大型工程设施、房屋等;抗震救灾能力是人类所采取的一系列动作,如应急救援、应急资源储备和调度策略等(杨继君等,2016)。
|
图 1 地震巨灾情景要素及其间关系 |
任何非常规突发事件情景均可以由致灾因子、孕灾环境、承灾体和抗震救灾能力来表示(龚艳冰等,2019;陈波等,2021)。为便于后续的情景推演分析,本文首先研究地震巨灾情景的四个基本要素及其相互关系。情景要素常见的结构形式包括知识元模型(仲秋雁等,2012)、petri网络模型(王循庆等,2014)、系统动力学模型(李勇建等,2015)、事件-承灾体二分网络(郄子君等,2020)等,其中知识元是知识管理的基础。知识元有助于从更加微观的角度认知地震巨灾及其演化规律,在表示离散性高且关联性高的知识元时具有较大优势。本文的知识元是一种知识表示方法(宋英华等,2018),如一个具体事物对象m的共性知识元可以表示为一个三元组,即
| $ K_m=\left(N_m, A_m, R_m\right), m \in M $ | (1) |
其中,M表示事物要素集,Nm表示已知事物,Am表示事物状态集,Rm表示状态变化关系集,这些属性可以用属性知识元来表示。
设属性a∈Am,其属性知识元可表示为
| $ K_a=\left(p_a, d_a, f_a\right) $ | (2) |
其中,pa为属性特征,da表示属性状态(如取值单位、取值类型、取值区间等),fa为属性函数。
设关系b∈Rm,其关系知识元可表示为
| $ K_b=\left(P_b, A_b, F_b\right) $ | (3) |
其中,Pb描述关系b所具有的特性,Ab为关系b的属性集,Fb为关系函数。
将知识元模型运用在地震巨灾情景中,设R为不同时刻情景Ri的集合,则有
| $ R=\left(Z_i, C_i, Y_i, N_i\right), i=1, 2, \cdots, n $ | (4) |
其中,Zi为致灾因子,Ci为承灾体,Yi为孕灾环境,Ni为抗震减灾能力。
1.2 情景-任务推演过程分析地震巨灾情景推演过程是各要素状态动态变化的过程。在数据确定情况下,按照通常的要素分析情景中各要素之间的关系,然后进行推演分析。然而在主观认识中,受事物信息不完全和主观条件限制等因素影响,人们对于灾害发生的条件和演化的认识存在不足。因此,几乎所有的地震巨灾情景推演都是在知识不完备或信息不完全、不确定条件下进行的。
在地震巨灾情景推演中,不确定性情景信息主要表现为随机性和不确定性。震害的随机性在地震情景描述中清晰明了,但由于事物之间的因果关系不确定,导致事件结果的可能性难以确定;不确定性因素在现实中无法被精确定义及描述,没有明确的边界,不是“非此即彼”,而是“亦此亦彼”,这主要源于客观信息的不完整,使人们无法形成精确的想法或概念,只能知道其处于某个范围或区间。针对地震巨灾的不确定性条件,本文采用模糊规则推理方法来解决情景推演问题。以知识元为基础,应用模糊推理方法来分析和推演震害信息,弥补震害信息不确定性的影响。
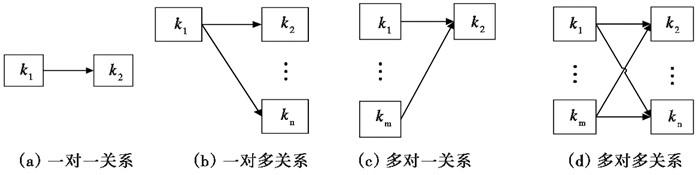
在孕灾环境和抗震救灾能力的耦合作用下,分析致灾因子和承灾体关系的变化是本研究的核心。在公式(4)中,4个因素中的致灾因子和承灾体的模糊关系可抽象为一对一关系(图 2(a)),即一种致灾因子对一种承灾体产生影响,并以此类推图 2中的其他关系。
|
图 2 知识元之间关系结构 |
为避免繁琐的推理,使用矩阵M代表致灾因子和承灾体的联系。设情景R有要素知识元k1,k2,…,kn,则M可表示为
| $ \boldsymbol{M}=\left[\begin{array}{cccc} m_{11} & m_{12} & \cdots & m_{1 n} \\ m_{21} & m_{22} & \cdots & m_{2 n} \\ \vdots & \vdots & \ddots & \vdots \\ m_{n 1} & m_{n 2} & \cdots & m_{n n} \end{array}\right] $ | (5) |
在本研究中,若知识元ki和kj存在作用关系,那么mij=1,否则为0。本文采用模糊关系来描述要素间的不确定关系,目的是为了解决要素之间相互作用是否导致特定结果的问题。模糊关系被视为常规关系的拓扑,用于衡量事物之间的关联程度(孟广武,2000)。
设有n个要素知识元素组成情景R,其对应的模糊关系表示为
| $ R=\left[\begin{array}{cccc} r_{11} & r_{12} & \cdots & r_{1 n} \\ r_{21} & r_{22} & \cdots & r_{2 n} \\ \vdots & \vdots & \ddots & \vdots \\ r_{n 1} & r_{n 2} & \cdots & r_{n n} \end{array}\right] $ | (6) |
其中,rij代表要素知识元ki对kj产生的影响程度,其取值范围为0~1。在模糊关系中,要素知识元之间具有作用关系,其隶属度在0~1之间,反映了相应要素间作用关系的影响程度。当要素之间具有确定的作用关系时,知识元的隶属度为1,否则为0。通过关系糊化处理所有要素知识元间的作用关系,可得到一个效用矩阵。其中,每个元素代表了一条情景推演的模糊规则,可表示为
| $ \text { Rule }[N]: \text { if } L\left\{P_1\left(W_1, F_1\right), P_2\left(W_2, F_2\right), P_3\left(W_3, F_3\right)\right\} \text {, then } Q(\theta, \tau) $ | (7) |
其中,N=1,2,…,n,表示模糊规则数量,n为前提条件的数量;L表示逻辑组合关系;Pi表示模糊规则第i个前提;Wi∈(0,1]表示子前提Pi的重要度,
模糊规则是能够表达不确定知识元及信息的一种方法,可用于辅助应急领域的决策。(张磊等,2016)。利用情景信息和模糊规则匹配进行情景推演,协助决策者在应急响应阶段进行应急决策。令MN(E,P)(0≤MN(E,P)≤1)表示情景不确定信息与第N条规则前提的匹配程度,即
| $ M^N(E, P)=\sum\limits_{i=1}^n w_i m\left(e_i, p_i\right) $ | (8) |
其中,m(ei,pi)用于衡量子前提的匹配度,具体计算方式根据实际应用特点定义。
在实际情况中,需首先满足条件
| $ m\left(e_i, p_i\right) \geqslant \lambda_i $ | (9) |
其中,λi为特殊匹配阈值,特殊前提匹配满足λi阈值后,才能进行规则匹配。针对第N条规则的模糊匹配时,若MN(E,P)≥τ模糊规则被触发,并得出结论Q,则存在概率
| $ \mu=M^N(E, P) \wedge \theta $ | (10) |
其中,∧表示连接两个命题时,两个命题必须同时为真,整个命题才为真。
在进行情景推演时,决策者需首先分析要素知识元,依据当前信息或数据将其实例化为相应的要素对象(例如学校、医院等)。随后,将情景的不确定性信息体现在属性描述中,增强推演的可靠性;根据模糊规则进行配对并估算要素对象之间相互影响的可能性,获得情景推演的效用矩阵。最后,通过推演分析的情景发展态势,按照高低进行排序,以提取能够适用于当前情景的应急任务。
2 案例分析 2.1 震害情景描述本文以A市为研究区,根据历史地震资料和地质结构的发展条件,假定在B区发生里氏7.0级地震,震源深度为20km,此次地震的最高烈度为Ⅸ度。
根据对A市历史地震震级与频次的分析与解读,加之A市具有人口较为稠密、建筑密集、经济要素积聚等城市特点,对于情景推演过程的刻画,主要是为了展现情景事件的发生机理以及发展过程中的关键节点及典型事件,但各阶段的应急响应特征及响应时间长短不尽相同。高建国(2004)将地震应急期划分为特急期、突急期和紧急期;詹承豫(2008)认为地震应急期一般可分为三个阶段,即初期救援阶段、中期安置阶段和后期恢复阶段;王海鹰等(2013)则将地震应急期划分成应急启动、紧急救援、过渡性安置等3个阶段;郭红梅等(2017)通过总结城镇地震应急处置案例,以应急任务为出发点将应急处置划分为4个阶段;随后张莹等(2022)对地震各阶段应急处置任务进行了动态调整。在实际地震灾害应对中,不仅需要考虑震后多长时间内完成哪些应急工作,还需要知道各工作之间的联动情况(王慧彦等,2021)。本文在情景分析的基础上,根据震后不同时期的应急处置特点,将整个震后情景划分为黑箱期阶段、应急初级阶段、紧急救援阶段、全面救援阶段和恢复重建阶段五个子情景,并对其进行情景推演及预测,如表 1所示。
| 表 1 各应急响应阶段震害情景描述汇总 |
运用知识元模型进行震害情景-任务推演分析,首先分析情景要素知识元及其相互作用关系;其次,基于情景信息对要素知识元进行实例化分析;最后,采用模糊推理方法分析情景推演中的不确定信息。根据上节灾害的描述,可以抽取出情境中的要素知识元,如表 2所示,分为致灾因子、承灾体、孕灾环境及抗震减灾能力四个方面。
| 表 2 情景要素知识元 |
假设情景中要素知识元致灾因子与承灾体之间的作用关系参考图 2(b)所示,这些关系能够借助式(3)得到,震害情景部分要素描述如表 3所示。以黑箱期阶段地震情景为例,构建地震与人员伤亡之间的数学模型,即
| $ \left\{\begin{array}{l} \varphi_1\left(\left\{\gamma_c, g, V_c\right\}, \{F\}, f_1\right)=0 \\ \varphi_2\left(\left\{F, F_{\max }, a, \sigma\right\}, \{\varphi, s d\}, f_2\right)=0 \end{array}\right. $ | (11) |
| 表 3 震害情景中致灾因子部分要素知识元 |
其中,F表示地震荷载,g为地震加速度峰值,α为房屋抗震设防水平,σ为建筑物倒塌率,φ为建筑物倒塌数量,γc为承载力特征值,Vc为承载力标准值,Fmax表示地震烈度,sd表示人员死亡数估计值。构建初始情景,表示为
| $ R_0=\left(\left(Z_0, C_0, Y_0, N_0\right)\right. $ | (12) |
其中,R0为在t0时刻要素知识元实例化后的要素对象集,将致灾因子、孕灾环境的实例化分为Z0、Y0,同一区域的社区1与社区2分别为实例化的建筑物要素c1、c2。这些对象之间存在着关系矩阵M。使用孙芳芳(2010)研究中的灰色关联度分析法确定子前提的权重,而隶属度则使用吕大刚等(2001)提出的模糊概率综合评价方法来确定。此时该区域的模糊规则式(7)可表示为
| $ \text { Rule[ 1] : if } P_1(0.6, 0.72), P_2(0.385, 0.67), P_3(0.47, 0.8) \text {, then } Q(0.255, 0.50) $ | (13) |
其中,P1表示该区域地震烈度,P2表示该区域建筑物抗震设防,P3表示该区域建筑物倒塌情况。假设t0时刻地震波位于A处,据式(5),初始情景S0的关联矩阵如下
| $ M_0=\left[\begin{array}{lll} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{array}\right] $ | (14) |
当t1时刻,地震波到达B处时,通过模糊概率综合评价法对情景信息进行处理,得出E={e1,e2,e3},其中e1=(地震烈度,0.69),e2=(建筑物抗震设防,0.54),e3=(建筑物倒塌率,0.8)。
用式(9)计算匹配度m(ei,pi),即
| $ m\left(e_i, p_i\right)=\frac{e_i^T p_i}{\left(p_i^T p_i\right) \vee\left(e_i^T p_i\right)} $ | (15) |
其中,∨为取大,则
同理,m(e2,p2)=0.806,m(e3,p3)=1,根据式(12)可得
| $ M^N(E, P)=\sum\limits_{i=1}^n w_i m\left(e_i, p_i\right)=0.90 $ | (16) |
根据式(10),可知人员伤亡的概率为μ=MN(E,P)∧θ=0.8。采用相同方法可以得到下一个情景S1的关系矩阵,即
| $ M_1=M_0 \vee R=\left[\begin{array}{lll} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{array}\right] \vee\left[\begin{array}{ccc} 0 & 0.8 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{array}\right]=\left[\begin{array}{ccc} 0 & 0.8 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{array}\right] $ | (17) |
根据情景推演分析结果可以得到:在t0时刻,地震波到达A处,由于与房屋满足空间约束并激活相应的模糊规则,对建筑物产生了影响;而在t1时刻,地震波到达B处,与房屋未满足时空约束。经计算可知,A处人员伤亡的可能性为0.8;而B处房屋不满足时空约束,故B处人员伤亡的可能性依然为0。通过情景推演的结果可以对此次震情做出基本判断:A处很可能出现建筑物破坏、人员伤亡等震害情景,B处建筑物基本完好、无人员伤亡。由此,地震应急相关单位需要对A处采取震情会商,制定相对应的救灾物资与准备方案,及时派出第一批应急救援队伍及医疗队伍,进行灾情汇总与信息公开,并对附近的交通进行管控及治安维护等地震应急响应措施。
在震害情景-任务推演分析过程中,以地震的灾害情景表达灾情状态,以地震应急响应任务作为应急的目标,通过情景推演梳理应急响应任务之间的相互关系,得到该时刻的应急响应措施。由于震害情景推演过程是一个复杂、繁琐的分析过程,具有很高的重复性,依据上述五个震害情景描述,选取黑箱期的人员伤亡情景为例进行详细情景推演,后续情景推演过程在此不做过多赘述。通过不同震害情景的推演结果,可以辅助决策者在情景信息不明确时预测事件发展趋势,更精确地得出地震应急任务,以便制定科学高效的应对措施。
2.3 地震巨灾应急响应任务生成地震巨灾应急响应任务是地震灾情与震后应急响应的纽带,其既是地震情景产生的后果,也是地震应急响应的依据。依据本文震害情景-任务推演思路,可以对若干地震情景推演结果的应对进行任务分解,从而在“情景”“任务”两者之间建立紧密的联系。针对构建地震巨灾情景可能造成的损失和后果情况,有针对性地开展应急任分析,列明应对地震巨灾必须的关键性任务要点,为后续地震应急响应提供科学依据。
通常来讲,震后各响应阶段的主要任务不是互不相干、相互独立的,在时间维度上往往是不同阶段的工作同时推进,每个阶段的应急任务有时也会与其前一阶段及后一阶段的任务同时实施。从不同响应阶段对应的震害情景出发,按时间序列设置响应任务流程,绘制地震应急响应任务推移图,其中包括地震应急响应阶段相关的各项应急任务,根据灾情的时间变化制定相应的应急任务,并将应急任务分阶段以鱼骨图的形式体现。
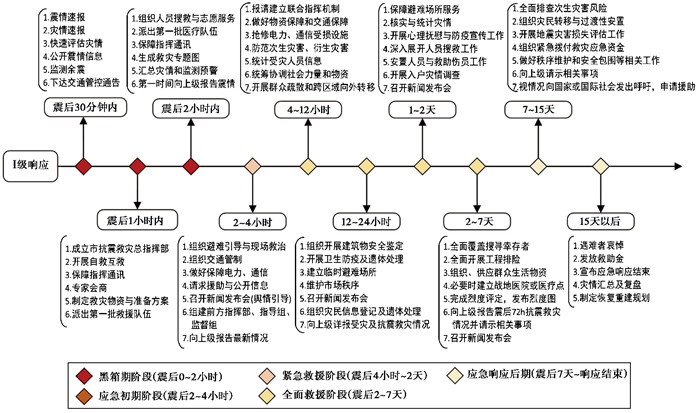
从任务流程和任务层级两个方面综合确定了地震巨灾应急响应推移图,如图 3所示。其体现了随着灾情时间推移地震应急响应的进程管理、各部门的应急任务及动向,通过共享震情信息,为实施协调联动提供地震灾害应急对策,便于决策者掌控抗震救灾工作的全局及决策调度的优先顺序,提高了地震应急处置能力。
|
图 3 地震巨灾应急响应任务推移图 |
基于对情景要素及其相互作用关系进行相对微观的分析,本文提供了一种基于知识元模型的情景表示模型。此外,进一步提出了情景推演的模糊推演方法,用于解决地震巨灾情景中存在的不确定性信息问题。将地震灾害情景全过程分为5个子过程,通过各知识元相互关联关系的模糊规则确定情景推演结论的可行性,并给出了地震巨灾情景推演中的应急任务。
但是,由于数据获取难度大、工作量繁重,当前的地震情景构建大多为定性和半定量模型,基于情景的地震应急任务设置的科学性与合理性还有待更精确的情景构建研究成果支持,主要原因有以下几方面:第一,目前我国超大型城市没有发生过大地震,缺乏实战经验,相关研究仍停留在借鉴其他城市地震实例;第二,情景构建数据不足,评价标准以定性居多,情景分析缺乏精确性;第三,超大型城市运行繁杂,次生衍生灾害链动态演化复杂,灾害间的耦合作用难以想象;第四,在应对地震灾害过程中,应根据灾害发生的实际情况采取相应的响应措施或进行灵活调整。
陈波、王芳、肖本夫, 2021, "情景-应对"型理论体系的发展及其在地震灾害应急管理中的应用探讨, 震灾防御技术, 16(4): 605-616. |
盖程程, 2020, 重大气象灾害多案例研究与情景构建方法探析, 城市与减灾, (5): 5-8. DOI:10.3969/j.issn.1671-0495.2020.05.003 |
高建国, 2004, 地震应急期的分期, 灾害学, 19(1): 11-15. DOI:10.3969/j.issn.1000-811X.2004.01.003 |
高山、王晗奕, 2021, 基于动态贝叶斯网络的突发公共卫生事件情景推演, 灾害学, 36(3): 28-34. |
龚艳冰、向林、刘高峰, 2019, 基于高斯过程回归模型的洪涝灾害损失预测研究——以重庆市为例, 长江流域资源与环境, 28(6): 1502-1510. |
郭红梅、张莹、陈维锋等, 2017, 多因素控制的城镇地震灾害应急处置模型研究, 震灾防御技术, 12(4): 882-892. |
李勇建、乔晓娇、孙晓晨等, 2015, 基于系统动力学的突发事件演化模型, 系统工程学报, 30(3): 306-318. |
刘健、杨仲江、杨虎等, 2016, 基于正态云模型的布达拉宫雷电灾害风险评估, 中国安全生产科学技术, 12(6): 100-104. |
刘铁民, 2012, 应急预案重大突发事件情景构建——基于"情景-任务-能力"应急预案编制技术研究之一, 中国安全生产科学技术, 8(4): 5-12. |
吕大刚、王光远, 2001, 基于损伤性能的抗震结构最优设防水准的决策方法, 土木工程学报, 34(1): 44-49. |
马鸿雁, 2021, 超大型城市应急管理的深圳探索, 中国应急管理, (10): 36-39. |
孟广武, 2000, 模糊数学的基本理论及其应用(Ⅲ)——截集、分解定理及扩展原理, 聊城师院学报(自然科学版), (2): 1-5. |
宋英华、刘含笑、蒋新宇等, 2018, 基于知识元与贝叶斯网络的食品安全事故情景推演研究, 情报学报, 37(7): 712-720. |
孙芳芳, 2010, 浅议灰色关联度分析方法及其应用, 科技信息, (17): 364-366. |
王海鹰、孙刚、欧阳春等, 2013, 地震应急期关键时间阶段划分研究, 灾害学, 28(3): 166-169. |
王慧彦. 2017. 城市功能系统安全视域下的地震情景研究. 见: 2017中国地球科学联合学术年会论文集(四十一)——专题79: 地震电磁扰动及其传播响应机理、专题80: 地震应急管理与研究. 北京: 中国和平音像电子出版社, 18~21.
|
王慧彦、王建飞、迟宝明等, 2021, 京津冀地区大震灾害应急专项预案编制研究, 城市与减灾, (6): 7-14. |
王慧彦、王建飞、刘晓静等, 2023, 基于情景构建的强震后京津冀地区协同应急机制研究, 地震研究, 46(1): 138-146. |
王慧彦、王建飞、张敬军, 2016, 基于情景构建的地震巨灾准备计划框架, 自然灾害学报, 25(6): 112-119. |
王循庆、李勇建、孙华丽, 2014, 基于随机Petri网的群体性突发事件情景演变模型, 管理评论, 26(8): 53-62. |
杨继君、佘廉, 2016, 面向多灾点需求的应急资源调度博弈模型及优化, 中国管理科学, 24(8): 154-163. |
詹承豫, 2008, 地震巨灾后抗震救灾的阶段划分及主要任务研究, 甘肃社会科学, (5): 44-47. |
张磊、王延章、陈雪龙, 2016, 基于知识元的非常规突发事件情景模糊推演方法, 系统工程学报, 31(6): 729-738. |
张文静、宋思然、王丽莉, 2018, 地震重大事件情景构建探讨研究, 地质与资源, 27(3): 298-301. |
张莹、郭红梅、赵真等, 2022, 基于序贯博弈与贝叶斯理论的地震应急分阶段动态决策方法研究, 中国地震, 38(2): 260-269. |
赵小伟、李永坤、杨忠山等, 2022, 超大型城市洪涝演变规律与调度模式分析, 水文, 42(3): 1-7. |
仲秋雁、郭艳敏、王宁等, 2012, 基于知识元的非常规突发事件情景模型研究, 情报科学, 30(1): 115-120. |
周愉峰、李志、李玉凤, 2020, 基于情景推演与故障贝叶斯网络的关键救灾设施中断机理, 自然灾害学报, 29(4): 173-184. |
朱伟、王晶晶, 2019, 北京的特大城市巨灾情景构建, 劳动保护, (3): 25-27. |
郄子君、荣莉莉, 2020, 面向灾害情景推演的区域模型构建方法研究, 管理评论, 32(10): 276-292. |
 2024, Vol. 40
2024, Vol. 40


